倾斜非圆曲线的数控车削宏程序的编制

　　2006年全国数控技能大赛北京决赛考试中，教师组数控车工软件考试中有一道特殊的宏程序题目，一段圆弧上均匀分布着多个首尾相连的椭圆曲线，给出宏程序要求找出其中的错误，图形示意图如图1所示(图形对比原题不一样，其中的尺寸是作者自己标注的)。

　　对于高水平的数控技能竞赛，非圆曲线的宏程序编制是必考的内容之一，一般选手都能掌握，但是一般非圆曲线的轴线都是与Z轴(或X轴)平行或者重合的(见图2)，这种非圆曲线的编程难度并不大，掌握非圆曲线加工的基本原理和学会曲线中心点的坐标偏移就可。但本文中所涉及到的题目则有其特殊之处，椭圆的轴线与Z 轴(或X轴)不平行，而是成一定的角度，整个椭圆是倾斜形状的，这种图形在数控铣床(或加工中心)上编程根本不存在难度，使用G68坐标旋转指令即可解决问题，但是在数控车削编程中没有G68坐标旋转指令，手工编程存在相当的难度，所以仅仅在软件仿真考试中给出程序并要求改正错误。

　　一、坐标旋转的数学基本原理

　　非圆曲线的宏程序编制都是基于对非圆曲线数学公式、图形特点的分析之上，所以良好的数学基础是编制宏程序的前提。要编制上面题目中有一定难度的宏程序，更需要深层次的数学知识。相同的题目，可以使用多种不同的数学方法解决，有简有繁，相应宏程序编制也不相同。

　　非圆曲线倾斜相当于把正常的坐标系和图形绕原点旋转了一个α角度所得到的图形和坐标系(见图3)。

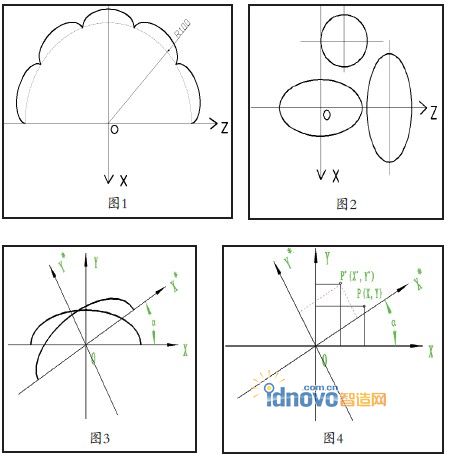
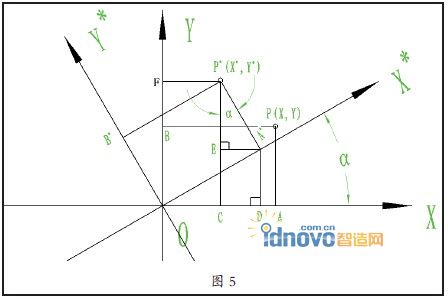
　　假设曲线上的一点P(见图4)，已知在XOY坐标系中的坐标为(X，Y)，坐标系和图形旋转一个角度α以后，P点旋转 后所在的位置为P*，P *点在原来XOY坐标系中的坐标为(X*，Y*)即为我们所求的坐标数值，由已知的P 点的坐标数值(X，Y)和旋转角度α通过多种数学处理方式和转换可以求出P*点 的坐标数值(X*，Y*)。

　　1.采用二维图形的变换矩阵进行旋转点的坐标计算

　　在计算机绘图基本原理中，二维图形的基本变换是通过矩阵运算进行的。在二维空间内，一个点的坐标可以表示为一个行向量|X  Y| ，一个二维空间点的坐标变换即为一个行向量|X  Y|和一个2×2阶变换矩阵的相乘运算，得到新点的坐 标(X*，Y*)。二维图形上的每一个点的处理都是如此。2×2 阶变换矩阵不同，可以得到图形的平移、镜像、旋转、比例和缩放等多种变换形式。

　　在本文讨论的题目中只涉及到图形的旋转变换，图形的偏移是通过其他方式处理的，因此只介绍图形的旋转变换矩阵，并且只介绍绕坐标原点旋转变换的2×2变换矩阵：

　　对于点P 坐标(X，Y )进行α角度的旋转变换，通过行向量|X Y|与变换矩阵T相乘运算以后，变换后P*点坐标为：

　　2.采用平面解析几何计算旋转点的坐标

　　图4中XOY坐标系中P点的坐标为(X，Y)，绕原点旋转α角度后得到X*OY*坐标系和点P*，要求出点P*在XOY坐标系中的坐标(X*，Y*)。

　　辅助线的作法(见图5)。

　　(1)过点P分别向X、Y 轴作垂线，得垂足A 、B，那么|OA|=X，|OB|=Y。

　　(2)过点P*分别向X*、Y *轴作垂线，得垂足A*、B*，那么|OA*|=X ，|OB*|=Y 。

　　(3)过点P*分别向X 、Y 轴作垂线，得垂足C、F 。

　　(4)过垂足点A*向P*C作垂线，得到垂足E，过垂足点A*向X轴作垂线，得到垂足D。分析图形中各线段的几何关系：

　　P*在XOY 坐标系中的坐标为(X* ，Y*)，X* = |OC|，Y* =|OF|，只要求出|OC|和|OF|的长度即可。

　　(1)X*坐标(|OC|长度)的求法。

　　在X坐标轴上，|OC |=|OD |-|CD|，在直角三角形中OA*D中(见图6)，已知角度α ，
|OA *|=X ，那么有：

　　|OD |=|OA*|·COS(α)=X ·COS(α) ①

　　在矩形CEA*D中，|CD| = |E A*|，在矩形OB*P*A* 中，

　　|P*A*|=|OB*|=Y，分析直角三角形P*A*E(见图7)，已知|P*A*|=Y和角度α，那么有：

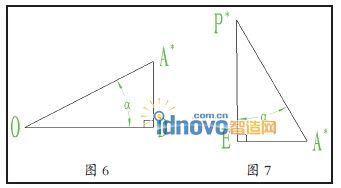
　　|EA*|=|P*A*|·SIN(α)=Y·SIN(α)=|CD| ②

　　P*点的X*坐标 |OC|=|OD|-|CD|=X·COS(α)-Y·SIN(α)。

　　(2)Y*坐标(|OF|长度)的求法。

　　在矩形OFP*C中，|OF|=|P*C|=|P*E|+|EC |，只要求出|P*E|和|EC|即可。

　　在直角三角形P*A*E中(见图7)，已知|P*A*|=|OB*|=Y角度α ，那么有：

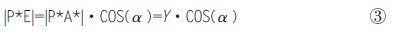
　　在矩形CEA*D中，|EC|=|A*D|，分析直角三角形OA*D(图6)，已知|OA*|=X 和角度α，那么有：

 　　P*点的Y*坐标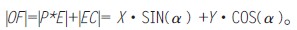从而确定P*点坐标求解公式为：

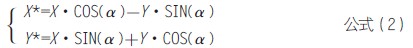
　　3.采用三角函数方法计算旋转点的坐标

　　已经知道平面上一点P的坐标为(X，Y)，|OP|为原点O 至P点的线段，|OP |线段与X 轴的夹角为θ(如图8所示)，那么有：

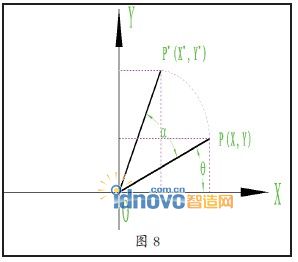
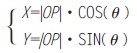
　　当坐标系绕原点旋转角度α以后，P*点为旋转后P 点的位置，旋转后|OP|线段的长度保持不变，|OP*|线段与X 轴的夹角为(α+θ)，那么有：

　　根据三角函数的运算法则：

　　最后得出P*点坐标求解公式为：

 　　数学分析总结：以上三种不同的数学方法对于旋转点的坐标计算有简有繁，但最终得出的公式(1)、公式(2)和公式(4)是统一的。介绍三种不同的数学处理方法的目的是为了适应不同数学基础和不同思路的编程人员能看懂并接受这个公式。虽然这三种方法的结果是统一的，但是在宏程序的编制处理上还有区别，前面两种数学方法可以使用相同的编程处理方式，但是最后一种数学处理方法的编程处理则有所不同，下面分别介绍。

　　二、单个倾斜椭圆的宏程序编制

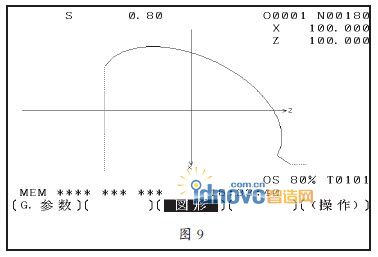
　　椭圆的长半轴50，短半轴30，长半轴与Z 轴的夹角30°，即椭圆倾斜了30°，工件坐标系的原点设在椭圆的中心，实际机床运行模拟的屏幕硬拷贝图形如图9所示。

　　程序的清单和注释如下：

　　N10 G98 S800 M03 主轴800r.p.m正转启动 N20 T0101 调用1号刀和刀具补偿 N30 G00 X60. Z50. 快速定位

　　N40 #1=30. X向半轴长度

　　N50 #2=50. Z 向半轴长度 N60 #3=30. 椭圆倾斜角度

　　N70 #4=50. Z 向变量#4的起始数值

　　N80 #24=SQRT[#2*#2-#4*#4] 普通椭圆上点X 坐标的计算

　　N90 #24=–#1*#24/#2 普通椭圆上点X 坐标的计算 N100 #26=#4 普通椭圆上点Z 坐标的计算 N110 #27=#26*SIN[#3]+#24*COS[#3] 倾斜椭圆上点X坐标的计算公式(1)Y*=X·SIN(α)+Y·COS(α) 车床使用ZX 坐标系，用Z 、X 代替X 、Y

　　N120 #28=#26*COS[#3]-#24*SIN[#3] 倾斜椭圆上点Z坐标的计算公式(1)X*=X·COS(α)-Y·SIN(α) 车床使用ZX坐标系，用Z、X代替X、Y

　　N130 G01 X[2.*#27] Z#28 F2000 直线段逼近椭圆(X 坐标变为直径值)

　　N140 #4=#4–0.5 Z 向变量#4循环递减步距0.5

　　N150 IF[#4GE[–#2]] GOTO80 循环判断语句 N160 G0 X100. X 向退刀

　　N170 Z100. Z 向退刀 N180 M30 程序结束

　　程序说明：程序中椭圆倾斜的角度α仅以30°为例，实际上的α角度有正有负，是任意的，包括0°、90°或180° 等特殊角度。

　　从程序中可以看出，倾斜椭圆(非圆曲线)宏程序的编制与普通椭圆(非圆曲线)宏程序的编制大体相同，不过仅仅增加了N110、N120两个坐标旋转公式的程序语句，这是根据前面两种数学方法得出的公式编制的宏程序，采用第三种方法编制的宏程序则不同。

　　程序清单以及注释如下：

　　N10 G98 S800 M03 主轴800r.p.m正转启动

　　N20 T0101 调用1号刀和刀具补偿

　　N30 G00 X60. Z50. 快速定位

　　N40 #1=30. X 向半轴长度

　　N50 #2=50. Z 向半轴长度

　　N60 #3=30. 椭圆倾斜角度

　　N70 #4=50. Z 向变量#4的起始数值

　　N80 #22=#4 普通椭圆上点Z 坐标的计算

　　N90 #23=SQRT[#2*#2-#4*#4] 普通椭圆上点X 坐标的计算

　　N100 #23=-#1*#23/#2 普通椭圆上点X 坐标的计算

　　N110 #25=ATAN[#23]/[#22] |OP |线段与椭圆长轴的夹角

　　N120 #21=SQRT[#22*#22+#23*#23] |OP |线段的长度

　　N130 #24=-2.0*#21*SIN[#25+#3] 倾斜椭圆上点X坐标的计算

　　N140 #26=#21*COS[#25+#3] 倾斜椭圆上点Z 坐标的计算

　　N150 G01 X#24 Z#26 F2000 直线段逼近椭圆

　　N160 #4=#4-0.5 Z 向变量#4循环递减步距0.5

　　N170 WHILE[#4EQ0] DO1 特殊处理程序段

　　N190 #21=#1 特殊处理程序段

　　N200 #24=-2.*#21*SIN[90.-#3] 特殊处理程序段

　　N210 #26=#21*COS[90.-#3] 特殊处理程序段

　　N220 G1X #24 Z#26 F2000 特殊处理程序段

　　N230 #4=#4-0.5 特殊处理程序段

　　N240 END1 特殊处理程序段

　　N250 IF[#4GE[-#2]]GOTO80 循环判断语句

　　N260 G00 X100. X向退刀

　　N270 Z100. Z 向退刀 N280 M30 程序结束

　　上面的宏程序是根据第三种数学处理方式编制的，与前面两种处理方式不同，它没有使用最后的计算公式(1)、(2)和(4)，而是使用了中间计算公式(3)进行编程。这种编程方式是计算出普通椭圆上每一个点P (X ，Z )与圆心连 线|OP |的长度，以及|OP |与长半轴的夹角θ ，加上旋转角度α 以后，再根据三角函数计算旋转点P* (X*，Z*)的坐标(如图8)。|OP|与长半轴的夹角θ是根据P点的坐标(X ，Z )，用反正切函数ATAN[X]/[Z]计算出来的，当变量Z(#4)为0时，

　　反正切函数ATAN[X]/[Z]是无定义的，不能求出角度的数值，所以在宏程序中有特殊处理程序段计算变量Z (#4)为0 时的角度。

　　上面的程序还有其他的解决办法，在求连线|OP|与长半轴的夹角θ时，可以不用反正切函数ATAN[X]/[Z]，而是使用反余弦函数ACOS[ ] ，这个函数不存在无定义的特殊点。程序相对会简化一些。

　　使用反余弦函数ACOS[ ]的程序清单及注释如下：

　　N10 G98 S800 M03 主轴800r.p.m正转启动

　　N20 T0101 调用1号刀和刀具补偿

　　N30 G00 X60. Z50. 快速定位

　　N40 #1=30. X向半轴长度

　　N50 #2=50. Z 向半轴长度

　　N60 #3=30. 椭圆倾斜角度

　　N70 #4=50. Z向变量#4的起始数值

　　N80 #22=#4 普通椭圆上点Z 坐标的计算

　　N90 #23=SQRT[#2*#2-#4*#4] 普通椭圆上点X 坐标的计算

　　N100 #23=-#1*#23/#2 普通椭圆上点X 坐标的计算

　　N120 #21=SQRT[#22*#22+#23*#23] |OP |线段的长度计算

　　N125 #25=ACOS[#22/#21] |OP |线段与椭圆长轴的夹角

　　N130 #24=#21*SIN[#25-#3] 倾斜椭圆上点X 坐标的计算

　　N140 #26=#21*COS[#25-#3] 倾斜椭圆上点Z 坐标的计算

　　N150 G01 X[-2.*#24 ] Z#26 F200 直线段逼近椭圆

　　N160 #4=#4-0.5 Z 向变量#4循环递减步距0.5

　　N250 IF[#4GE[-#2]] GOTO80 循环判断语句

　　N260 G00 X100. X 向退刀

　　N270 Z100. Z 向退刀 N280 M30 程序结束

　　可以看出，使用反余弦函数ACOS[ ]比较使用反正切函数ATAN[X]/[Z]在程序要简化许多，同时也可以知道，同一个加工要求的图形，可以有多种编程方法和途径解决。

　　三、圆弧上均布椭圆的宏程序编制

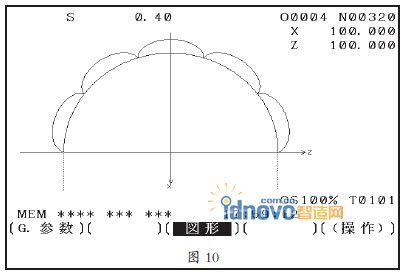
　　对于图1中的加工图形，实质上是椭圆圆心在不同点上、长半轴倾斜角度不同的首尾相连的多个椭圆曲线，其核心仍然是倾斜椭圆的编程处理。实际机床运行模拟的屏幕硬拷贝图形如图10所示。

　　程序清单以及注释如下：

　　N10 G98 S300 M03 主轴800r.p.m正转启动

　　N20 T0101 调用1号刀和刀具补偿

　　N30 G00 X0 Z100. 快速定位

　　N40 G2 X0 Z-100. R100. F300 模拟加工R 100的圆弧，方便观察均布椭圆的加工过程

　　N50 #1=100. 圆弧的半径

　　N60 #2=5. 均布椭圆的个数

　　N70 #3=180. 圆弧对应的圆心角度

　　N80 #4=#3/#2 每个椭圆对应的圆心角度

　　N90 #5=#1*COS[#4/2.] 椭圆中心点与原点的距离

　　N100 #6=#1*SIN[#4/2.] 椭圆的长半轴计算

　　N110 #7=#6*0.6 椭圆的短半轴，因为没有尺寸，暂定 为长半轴的0.6倍

　　N120 #8=#4/2. |OP |连线与Z轴的起始夹角

　　N130 #21=1. 椭圆个数的计数器

　　N140 #9=#5*COS[#8] 椭圆中心点的Z 坐标计算

　　N150 #11=-#5*SIN[#8] 椭圆中心点的X 坐标计算

　　N160 #12=90. -#8 椭圆长半轴倾斜的角度计算

　　N170 #15=#6 椭圆Z 向变量#4的起始数值

　　N180 #16=SQRT[#6*#6-#15*#15] 普通椭圆上点X坐标的计算

　　N190 #16=-#16*#7/#6 普通椭圆上点X 坐标的计算

　　N200#17=#15*SIN[#12]+#16*COS[#12] 倾斜椭圆上点X坐标的计算

　　N210 #18=#15*COS[#12] -#16*SIN[#12] 倾斜椭圆上点Z 坐标的计算

　　N220 #18=#18+#9 椭圆上点Z 坐标的偏移计算

　　N230 #17=#17+#11 椭圆上点X 坐标的偏移计算

　　N240 G01 X[2.*#17] Z#18 F300 直线段逼近椭圆

　　N250 #15=#15-#6/40. Z向变量#4循环递减步距#6/40

　　N260 IF[#15GE[-#6]] GOTO180 循环判断语句

　　N270 #8=#8+#4 |OP |连线与Z轴的夹角循环递增

　　N280 #21=#21+1. 椭圆个数计数器递增1.0

　　N290 IF[#21LE#2]GOTO140 循环判断语句 N300 G00 X100. X 向退刀

　　N310 Z100. Z 向退刀 N320 M30

　　程序结束

　　在上面的宏程序中，有几点注意事项：

　　(1)这是在凹圆弧上的多个凹椭圆曲线，加工区域都是在X轴的负值区域，在实际切削加工中是不可能出现的。实际切 削时，可以把椭圆上的坐标点向X 向(或Z向)做相应的偏移处理。另外，因为图样条件都是假设，没有考虑刀具的角度以及加工干涉的问题。

　　(2)本程序中使用了双重循环，内循环控制单个椭圆曲线的加工(本程序加工的是半个椭圆，当然可以改变参数，加工起点和终点不同的部分椭圆)。外循环控制椭圆中心点的坐标和椭圆长轴倾斜角度的变化，最终加工出连续的椭圆曲线族。

　　(3)本程序中还有一个特殊之处是在椭圆曲线的编程时，Z向变量#15的步距，一般椭圆曲线宏程序编制时取的步距为0.1、0.2、0.4、0.5…等规整的数值，但是在本程序中不可以，因为椭圆的长半轴的计算出的数值不是整数值，所以步距取#6/40.0，即步距为长半轴的1/40，也可以说是用40段直 线段逼近椭圆曲线。分母的数值越大，步距越小，曲线加工的精度越高。如果使用规整数值0.1、0.2、0.4、0.5…，有可能出现椭圆曲线的末端加工“欠切”和“过切”的现象。

　　(4)本程序中使用的是坐标旋转公式(1)、(2 )和(4)，没有使用公式(3)，其原因是：

　　◎使用公式(3)必须使用反余弦函数ACOS[ ](或反正切 函数ATAN[X]/[Z])，而这两个反函数都有无定义点(ACOS[-1.0]在实际机床数控系统中也无定义，会报警出错)。对于无定义点需要特殊程序段处理，增加了程序段数量和编程难度。

　　◎使用反余弦函数ACOS[ ](或反正切函数ATAN[X]/[Z])时，需要多次数学运算，在连续椭圆曲线加工运算时会出现累积误差，导致最后一个椭圆曲线“欠切”，但对单个椭圆曲线不会出现这种情况。

　　◎公式(1)、(2)和(4)中只有单次数学运算，不存在无定义点，没有累积误差，编程简单，推荐使用。本文使用公式(3)编程只是增加一种编程思路，起对比分析作用。

　　四、程序分析总结

　　(1)宏程序的功能是强大的，但逻辑思维性强，需要考虑多个参数的变化及其相互的关系，而数学培养锻炼的正是人的思维的逻辑性、条理性和敏锐性，良好的数学基础是掌握并熟练运用宏程序的前提条件。

　　(2)通过三种数学处理方法得出的坐标旋转点的计算公式(1)、(2)和(4)具有通用性，与具体的曲线形式无关，即公式(1)、(2)和(4)对于倾斜的椭圆、双曲线、抛物线、正(余)弦曲线等非圆曲线都适用。

　　(3)有些书籍中把宏程序称为“自由编程”是有一定的道理的，每个人都可以根据自己不同的数学基础，对于同一图形不同的解读，以不同的思路，编制出不同的加工程序，而最终得到的加工结果是相同的。这也验证了数控加工的一个基本原则：“数控加工没有惟一的途径，只有惟一的结果”。